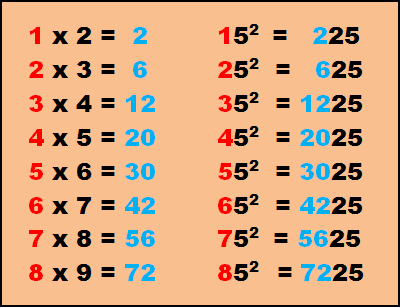FRANCOIS VIETE PI

CURIOSIDADES CINCOS AL CUADRADO

CURIOSIDADES MATEMÁTICAS 17

CURIOSIDADES NUMERO CICLICO

PROGRAMACIÓN LINEAL - OPTIMIZACIÓN LINEAL

PROGRAMACIÓN LINEAL

OPTIMIZACIÓN LINEAL (ENFOQUE GEOMÉTRICO)

En un problema de programación lineal se requiere encontrar el máximo o mínimo de alguna expresión  algebraica cuando las variables de ésta expresión están sujetas a un número de desigualdades lineales. El ejemplo simple siguiente es típico de tales problemas.

EJEMPLO 1 (UTILIDAD MÁXIMA)

Una compañía fabrica dos productos, X y Y. cada uno de estos productos requiere cierto tiempo en la línea de ensamblado y otro tiempo más en el departamento de acabado.  Cada artículo del tipo X requiere 5 horas  de ensamblado y 2 horas de acabado, mientras que cada artículo del tipo Y requiere 3 horas de ensamblado y 4 horas de acabado. En cualquier semana, la empresa dispone de 105 horas en la línea de ensamblado y  70 horas en el departamento de acabado. La empresa puede vender todos los artículos que produce y obtener una utilidad de $200 por cada artículo de X y $160 por cada artículo de Y. calcule el número de artículos de cada tipo que deberían fabricarse a la semana con objeto  de maximizar la utilidad total.

SOLUCIÓN.

Por lo regular es conveniente al manejar problemas de este  tipo resumir la información en una tabla.

	ENSAMBLADO	ACABADO	UTILIDAD
X	5	2	200
Y	3	4	160
DISPONIBILIDAD	105	70

Suponga que la empresa produce x artículos del tipo X a la semana y y artículos del tipo Y a la semana. Entonces el tiempo necesario en la línea de ensamblado será de 5x horas en el caso  del producto X y  3y horas para el producto Y, o  (5x + 3y) horas en total. Dado que solo se pueden disponer de 105 horas, debemos tener que 5x + 3y ≤ 105.

De manera similar, se requieren 2x horas en el departamento de  acabado por cada x artículos del producto X y 4y por cada y artículos del producto Y. el número total de horas, 2x + 4y, no pueden exceder las 70 de que se dispone, de modo que tenemos la segunda condición, 2x + 4y ≤ 70.

Cada artículo del tipo X genera una utilidad de $200, de modo que  x artículos producen 200x dólares de utilidad. En forma análoga, y artículos del tipo Y producen 160y dólares de utilidad. Así, la utilidad semanal total  P (en dólares) está dada por

P = 200x + 160y.

Por consiguiente, podemos restablecer el problema en los términos siguientes:

Encuentre los valores x y y que maximizan la cantidad P = 200x + 160y  cuando x y y están sujetas a las condiciones:

5x + 3y ≤ 105,          2x + 4y ≤ 70,            x ≥ 0,       y           y  ≥ 0    

Este ejemplo es un  problema característico de programación lineal. Tenemos una  expresión P = 200x + 160y  que es lineal en las variables x y y, y deseamos encontrar el valor máximo de P cuando x y y satisfacen las desigualdades. Un problema más general podría incluir más de dos variables  y un número mayor de desigualdades que las cuatro de este ejemplo, pero de cualquier manera este ejemplo es bastante representativo de los problemas del área de programación lineal.

Al analizar cualquier problema de programación lineal, en especial cuando solo intervienen dos variables, con frecuencia es útil un enfoque geométrico.   
     

Consideremos las desigualdades vistas. El conjunto de puntos (x,y) que satisface todas las desigualdades aparece sombreado en la figura 1. Esta región sombreada representa el conjunto de soluciones factibles, esto es, el conjunto de valores de x y y que la empresa puede adoptar. No se puede tomar, cualquier punto (x,y) situado afuera de esta región sombreada.

FIGURA 1

Por ejemplo, consideremos el punto x=12, y=14, el cual está fuera de la región factible. A fin de producir  12 artículos de tipo X  y 14 artículos del tipo Y  se requerirán          12(5) + 14(3) = 102 horas en la línea de ensamblado y 12(2) + 14(4) = 80 horas en el departamento de acabado. Si bien, esto no excedería las horas disponibles en la línea de ensamblado, si sobrepasa aquellas disponibles en el departamento de acabado; de modo que no está dentro del programa de producción posible.

Consideremos ahora el conjunto de valores x y y que conducen a alguna utilidad fija. Por ejemplo, dado a P el valor 4000, advertimos que x y y deben satisfacer la ecuación.

                                   200x + 160y=4000

Todos los valores de x y y que satisfacen esta ecuación producen una utilidad de $4000 a la semana. Esta es la ecuación de una línea recta que corta el eje x  en el punto (20,0) y al eje y  en el punto (0,25), como se aprecia en la figura 2. Parte de esta línea pasa por la  región de soluciones factibles. Debido a esto, concluimos que le es posible a la empresa lograr una utilidad de 4000 dólares a la semana. Puede realizar esto eligiendo cualquier valor de  (x,y) situados en los segmentos AB  que aparece en la figura 2.

FIGURA 2

Por otra parte consideremos P=6000. Los valores correspondientes de x y y deben satisfacer 200x + 160y=6000, que otra vez es la ecuación de una  línea recta, esta vez corta a los ejes de coordenadas en los puntos (30,0) y (0.37.5). Esta línea recta no pasa por la región sombreada de soluciones factibles (véase la figura 2) y por ello no es posible a la empresa obtener una utilidad tan grande como $6000 a la semana. La utilidad máxima posible debe estar en algún lugar entre $4.000 y $ 6.000 a la semana.

El conjunto de puntos (x,y) que conducen a una utilidad dada P satisfacen la ecuación 200x + 160y=P. esta ecuación, para P fija, tiene como grafico una línea recta en el plano xy llamada línea de utilidad constante  o curva de indiferencia . Las dos líneas que aparecen en la figura 2  son líneas de utilidad constante que corresponden a los valores P=4000 y P=6000.

La ecuación de una línea de utilidad constante puede escribirse de la forma

                           160y = P – 200x

O bien      y = -   5 x  +    P   

                             4         160

Por tanto la línea tiene pendiente  -5/4  y ordenada al origen P/160. Es una propiedad importante que la pendiente de cualquier línea  de utilidad constante es la misma sin importar  el valor de P.  Esto significa que todas las líneas de utilidad constante son paralelas entre sí. A medida que el valor de P se incrementa, la línea de utilidad  máxima correspondiente se aparta del origen (la ordenada al origen aumenta), siempre con la misma pendiente.

A fin de obtener la utilidad máxima, debemos alejar la línea de utilidad constante del origen  hasta que solo toque el extremo de la región de soluciones  factibles.

Es claro por la figura 2 que la línea de utilidad máxima es la que pasa por la esquina C situada en la frontera de la  solución factible. Los valores de x y y en C dan los  volúmenes de producción de los dos productos X y Y que conducen a la utilidad máxima.

El punto C es la intersección de las dos líneas  rectas que acotan la región factible. Sus coordenadas se obtienen resolviendo las ecuaciones de estas dos líneas, 5x + 3y = 105 y      2x + 4y = 70. Resolviendo estas ecuaciones, encontramos que x=15 y y=10. Por consiguiente, la utilidad máxima es cuando la empresa produce 15 artículos del tipo X y 10 artículos del tipo Y a la semana. La utilidad semanal máxima está dada por

P_max   =  200x + 460y

            = 200(15) + 160(10)

            = 4600

La utilidad máxima es por tanto $4.600.

El procedimiento usado  en la resolución de este problema también puede emplearse cuando ocurre un número mayor de desigualdades.

Bibliografía: MATEMATICAS  APLICADAS A LA ADMINISTRACION Y A LA ECONOMIA / Jagdish C.  Arya/Robin W, Lardner / Prentice Hall / tercera edición .

APLICACIONES DE MATRICES

SUMA DE MATRICES

EJEMPLO 1

MATRIZ DE PRODUCCIÓN

Una empresa que fabrica televisores produce tres  modelos con distintas características  en tres tamaños diferentes.  La capacidad de producción  (en miles) en su planta número uno  está dada por la matriz A.

(a)  ¿Cuál es la capacidad de producción total en las dos plantas?

(b)  ¿si la empresa decide incrementar  su producción en la planta número uno  en un 20 % . ¿Cuál será la nueva producción en la planta?

 

CURIOSIDADES RAIZ DIGITAL

CURIOSIDAD 1 + 3 = 2^2

APLICACION DE ECUACIONES ORO

Ejemplo 2

Un joyero tiene dos barras de aleación de oro; una es de 12 quilates y la otra, de 18 (el oro de 24  quilates es oro puro, el de 12  quilates corresponde a  12/24  de pureza, el de 18 a  18/24 de pureza y así sucesivamente.)

¿Cuántos  gramos de cada aleación se deben  mezclar para obtener 10 gramos de oro de 14 quilates?

SOLUCION:

Sean:             X = número de gramos utilizados de oro de 12 quilates

                       Y = número de gramos utilizados de oro de 18 quilates

                                    X + Y = 10

            (12/24) X + (18/24)Y = (14/24)(10)

                 (1/2) X + (3/4) Y = (7/12)  (10)
            12(  (1/2) X + (3/4)Y) = 7   (10)

              (12/2) X +(36/4) Y = 70 

6X + 9Y = 70

Luego nos quedan dos ecuaciones

(1)  X + Y = 10

(2)  6X + 9Y = 70

Despejamos  X en la ecuación (1)

                        X = 10 –Y

Reemplazamos X en la ecuación (2)

                        6(10 – Y) + 9Y = 70

                          60 – 6Y + 9Y = 70

                                 -6Y + 9Y = 70 – 60

                                           3Y = 10

                                    Y =10/3 = 3,33    gramos de aleación de 18 quilates

Si        X + 3,33= 10

                      X = 6,66    gramos de aleación de 12 quilates

CURIOSIDADES MATEMATICAS 15 TABLAS X 25

APLICACIONES DE SISTEMAS DE ECUACIONES LINEALES

PLICACIONES DE  SISTEMAS DE ECUACIONES  LINEALES
MEZCLAS

La tienda el sol que se especializa en todo tipo de frituras, vende cacahuates a $0.70 la libra y almendras a $1.60 la libra. Al final del mes, el propietario se entera que los cacahuates no se venden bien y decide mezclar cacahuates con almendras para producir una mezcla de 45 libras, que venderá a $1.00 la libra.

¿Cuántas libras de cacahuates y de almendras deberá mezclar para mantener los mismos ingresos?

SOLUCIÓN

Sea x las libras de cacahuates que la mezcla contiene y y las libras correspondientes de almendras. Dado que el peso total es de 45 libras,

X + y = 45

El ingreso de x libras de cacahuate a $0.70 la libra es de 0.7x dólares, y el ingreso de y libras de almendras a $1.60 la libra es de 1.6y dólares. El ingreso obtenido de la mezcla de 45 libras a $1.00 la libra será de $45. Dado que el ingreso de la mezcla deberá ser el mismo que el de las frutas separadas, tenemos la ecuación siguiente.

Ingreso de los cacahuates + ingreso de las almendras = ingreso de la mezcla

0.7x + 1.6y = 45

7x +16y = 450

Libras de cacahuate + libras de almendras = libras de mezcla

X + Y = 45

De esta manera, llegamos al sistema de ecuaciones lineales siguiente.

X + Y = 45

7x +16y = 450

De la primera ecuación, obtenemos que x = 45 – y. luego sustituimos este valor de x en la ecuación de abajo y despejamos y.

7(45 – y) +16y = 450
315 –7y + 16y = 450

9y = 450 -315 =135

Y =15

Por tanto, x = 45 – y = 45 – 15 = 30.

En consecuencia 30 libras de cacahuate deberán mezclarse con 15 libras dealmendras para formar la mezcla.

CURIOSIDADES MATEMÁTICAS 14

CURIOSIDADES MATEMÁTICAS 1 + 2 ^2

APLICACIONES DE DESIGUALDADES 2

DECISIONES DE FABRICACIÓN

El administrador de una fábrica debe decidir  si deberán producir sus propios empaques, que la empresa ha estado adquiriendo de proveedores externos a U.S. $1,10 cada uno. La fabricación de los empaques incrementaría  los costos generales de la empresa en  U.S. $800  al mes y el costo de material y de mano de obra  será de U.S. $0,60 por cada empaque. ¿Cuántos empaques deberá usar la empresa al mes para justificar la decisión  de fabricar sus propios empaques?

SOLUCIÓN

Sea x el número de empaques utilizados por la empresa al mes. Entonces el costo de adquirir x empaques  a  U.S. $ 1,10  cada uno es  de 1,10x dólares.  El costo de fabricar x empaques es de U.S. $0,60 por empaque más costos generales de U.S. $800 al mes, de modo que  el costo total es

            0,60x + 800

Para justificar la fabricación de los empaques por la empresa misma, debe ser cierta la desigualdad siguiente.

                     Costo de adquisición > costo de fabricación

                                                  1,10x > 0,60x + 800

     1,10x – 0,60x > 800

                  0,50x > 800

                         X > 1600

En consecuencia,  la empresa debe usar al menos 1601 empaques al mes para justificar el fabricarlos.  

CURIOSIDADES MATEMÁTICAS 12

CRITERIOS DE DIVISIBILIDAD
2	Todos los números pares
3	La raíz digital es divisible por 3 ( la raíz digital se encuentra sumando todos los dígitos de un número. Si la suma es de varios dígitos repita hasta que tenga un digito solo)  45678 : 4+5+6+7+8 = 30 :    3+0 = 3
4	Tome los últimos dos dígitos en el número y divídalos a la mitad, si el cociente es par, el número es divisible por 4
5	El ultimo digito es 5 o 0
6	El número es par  y la suma digital es 3, 6 o 9
7	Reste 2 veces el ultimo a los otros dígitos. Ejemplo. 224 :  22-8 =14 y 14 es divisible por 7
8	Un número es divisible por 8 si la suma de la cifra de las unidades más el doble de la cifra de las decenas más el cuádruple de la cifra de las centenas es 0 o múltiplo de 8 (El número formado por sus tres últimas cifras es divisible por 8) Ejemplo 1: ¿Es divisible por 8 el número 1982? Las unidades son 2, las decenas 8 y las centenas 9; Aplicando criterio la suma 2 + 8x2 + 9x4 = 2 + 16 + 36 = 54 no es múltiplo de 8, por consiguiente no  es divisible por 8.
9	La raíz digital es  9 Ej: 378; 3+7+8= 18;  1+8=9  Si es divisible por 9. Ej: 12150; 1+2+1+5+0= 9 si es divisible por 9
10	El número termina en cero
11	Para cualquier número, sume los números alternados y réstele la suma de los potros números, si la respuesta es cero o múltiplo de 11, entonces el número es divisible por 11.   Ejemplo: 1054031 ;  1+5+0+1= 7   menos 0+4+3=7   da cero, entonces si es divisible por 11
12	El número debe ser divisible por 3 y por 4
13	Sume cuatro veces el ultimo digito a los dígitos restantes, si el numero es divisible por 13 entonces el número es divisible , aplique esta regla una y otra vez si es necesario. Ejemplo:206635 ; 20663 + (4x5)=20683;  2068 + (4x3)= 2080;  208 + (4x0)= 208 ; 20+(4x8)=72  y 52 = 13 x4, por lo tanto 206635 es divisible por 13.
14	Si es par y divisible por 7
15	Es divisible por 3 y termina en 0 o 5.
16	Divida el número a la mitad 3 veces y si el resultado es par, entonces el número es divisible por 16
17	Reste 5 veces el ultimo digito del resto,  repita el procedimiento  hasta que tenga un número múltiplo de 17 .  EJEMPLO;167.858 ; 16785 – 40= 16745;  1674-25=1649 ; 164-45=119  y 119 es 17x7 entonces  167.858 es divisible por 17.
18	Si es par y su raíz digital es 9
19	Sume dos veces el ultimo digito al resto, ejemplo 1.615; 161+10=171;  17+2=19 entonces si es divisible por 19
20	El digito de las decenas es par y termina en cero.